引用本文
鲁圣国, 唐新桂, 伍尚华. 铁电材料中的大电卡效应. 无机材料学报, 2014, 29(1): 6-7
LU Sheng-Guo, TANG Xin-Gui, WU Shang-Hua, ZHANG Qi-Ming. Large Electrocaloric Effect in Ferroelectric Materials. Journal of Inorganic Materials, 2014, 29(1): 6-7  
Permissions
Copyright©2014, Editorial Board of Journal of Inorganic Materials
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
铁电材料中的大电卡效应
鲁圣国1, 唐新桂2, 伍尚华3
1. 广东工业大学 材料与能源学院, 广州 510006
2. 广东工业大学 物理与光电工程学院, 广州 510006
3. 广东工业大学 机电工程学院, 广州 510006
4. Department of Electrical Engineering and Materials Research Institute, The Pennsylvania State University, University Park, PA 16802, USA

鲁圣国(1963-), 男, 博士, 教授. E-mail:sglu@gdut.edu.cn

基金:National Natural Science Foundation of China (51372042)
摘要

电卡效应在实现高效率和小尺寸的固态制冷器件方面具有巨大的潜力。本文介绍了获得大电卡效应的热力学原理, 评述了近年来电卡效应的实验表征工作, 发展了一种直接测量电卡效应熵变或温度变化的方法。结果表明: 驰豫型铁电体聚合物和一级相变聚合物材料表现出较大的电卡效应。综合最近在BaTiO3单晶和多层陶瓷电容器的工作, 以及铁电制冷器件的尝试, 电卡效应表现出诱人的应用前景。

关键词: 铁电材料; 单晶; 陶瓷; 聚合物; 电卡效应; 制冷器件; 综述
中图分类号:TM22   文献标志码:A    文章编号:1000-324X(2014)01-0006-07
Large Electrocaloric Effect in Ferroelectric Materials
LU Sheng-Guo1, TANG Xin-Gui2, WU Shang-Hua3, ZHANG Qi-Ming4
1. School of Materials and Energy, Guangdong University of Technology, Guangzhou 510006, China
2. School of Physics and Optoelectronic Engineering, Guangdong University of Technology, Guangzhou 510006, China
3. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China
4. Department of Electrical Engineering and Materials Research Institute, The Pennsylvania State University, University Park, PA 16802,USA
Abstract

The electrocaloric effect (ECE) in polar materials shows great potential in realizing high efficient solid-state cooling devices with a smaller size and high efficiency. The thermodynamic theory was introduced in order to achieve a large ECE in ferroelectrics. The previous experimental researches were reviewed and discussed. A novel method to directly measure the ECE entropy change and temperature change was developed. Results indicated that the relaxor ferroelectric polymers and first-order phase transition polymers demonstrated larger ECE. Recently published larger electrocaloric effect in BaTiO3 crystal and multilayer ceramic capacitors, and the prototype ferroelectric cooling devices reveal attractive application prospects in the near future.

Keyword: ferroelectric materials; single crystal; ceramics; polymers; electrocaloric effect; cooling devices; review

制冷是人们日常生活中必不可少的事情, 从水果、蔬菜、肉类保鲜, 到空调的使用, 再到医用方面的器官冷藏、器官移植、核磁共振成像等, 都需要制冷。普通的压缩机制冷的方法已经差不多到了其极限, 并且其排出的有机气体, 直接破坏嗅氧层, 引起了全球性的温室效应, 对环境的破坏作用已越来越受到人们的重视。寻找新的制冷方式成为一项刻不容缓的任务。

电卡效应(Electrocaloric Effect)是在极性材料中因外电场的改变从而导致极化状态发生改变而产生的绝热温度或等温熵的变化[ 1, 2, 3]。由于电卡效应直接与极化强度的变化相关, 因而强极性的铁电材料能产生较大的电卡效应。对极性材料施加电场, 材料中的电偶极子从无序变为有序, 材料的熵减小, 在绝热条件下, 多余的熵产生温度的上升。移去电场, 材料中的电偶极子从有序变为无序, 材料的熵增加, 在等温条件下, 材料从外界吸收热量使能量守恒。或在绝热条件下, 不足的熵导致材料温度的下降。这就是电卡效应的制冷原理。

对于一个理想的制冷循环, 电场移去时电卡材料能从接触的负载吸收热量(等温熵变)。然后电卡材料与负载分开, 此时, 若对电卡材料施加电场, 材料的温度将会升高(绝热温变)。将电卡材料与散热片接触, 多余的热量将要释放出去, 使得电卡材料的温度与室温一致。然后, 电卡材料与散热片断开, 并与负载相接触。移去电场, 电卡材料的温度 降低, 并从负载处吸收热量。重复整个过程, 负 载的温度会不断降低。这就是电卡制冷机的基本原理。由于在热循环过程中, 电卡材料的熵变和温变都起到了作用, 两者对热循环都是非常重要的。

电卡效应的研究可以追踪到上个世纪30年代, 两位德国科学家Kobeko及Kurtschatov首先测量了罗息盐的电卡效应[ 4], 得到了定性结果, 但没有数据报道。 1963年, 两位美国科学家重复了他们的实验, 并在22.2 ℃, 1.4 kV/cm的条件下, 测得绝热温度变化为0.0036 ℃[ 5]。由于铁电体等极性材料性能的限制, 电卡效应的研究得到的绝热温度的变化都小于1 ℃[ 6, 7, 8, 9, 10]。 这主要是由于体材料的击穿电场较低, 材料的选择范围也相对较窄。

与此同时, 磁卡效应的研究取得了一系列成果, 获得了数种被称为巨磁卡效应的材料体系, 如Gd5(Si xGe4- x)[ 11]、Tb5Si2Ge2[ 12]、MnAs1- xSb x[ 13]、La(Fe1- xSi x)13[ 14]、La(Fe1- xSi x)13H y[ 15]、MnFeP xAs1- x[ 16]及Ni2± xMn1± xGa[ 17]。这些材料的单位磁场的绝热温度变化达到4 ℃/T(T-特斯拉)。相应地, 磁卡制冷机也被研制出来。磁卡制冷与电卡制冷都是利用固态相变制冷, 在原理上没有本质的区别。磁卡效应的优点是磁场不必与样品接触, 并且可以非常强而不考虑击穿的问题; 缺点是磁场的产生需要磁铁, 这阻碍了制冷器件的小型化, 在设计上也很不灵活。电卡效应电场的设计取决于高压端的形状, 在设计上非常灵活多样。

本文将通过介绍电卡效应的热力学理论, 以及在铁电陶瓷、单晶、铁电薄膜以及铁电聚合物中的研究现状, 探索提高电卡效应的途径, 预测电卡制冷器件的应用前景。

1 电卡效应的热力学理论
1.1 Maxwell关系

对于介电材料, 弹性Gibbs自由能 G可以展开为温度 T、熵 S、应力 X、应变 x、电场强度 E和电位移 D的函数, 即

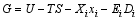(1)

这里 U为系统的内能, 式(1)右边后两项采用Einstein求和记法。式(1)的微分形式为:

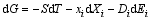(2)

根据式(2), 在其它两个变量为常数时, 熵 S、 应变 xi及电位移 Di可以表示为:

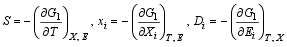(3)

因此, 对( S, T)和( D, E)两组参数, Maxwell关系可以导出为[ 1]:

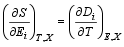(4)

或写为:

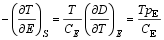(5)

其中, CE为比热, pE为热释电系数。式(4)和(5)表示温度和应力恒定时的电卡系数等于电场和应力恒定时的热释电系数。同样地可以得到

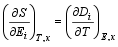(6)

即温度和应变恒定时的电卡系数等于电场和应变恒定时的热释电系数。

根据式(4), 对于电卡材料, 在应力或应变为常数时, 等温熵变和绝热温变可以表示为:

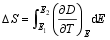(7)

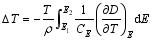(8)

从式(7)和(8)可知, 为了得到较大的等温熵变和绝热温变, 电卡材料需要有较大的热释电系数和较高的抗击穿电场强度。在等温熵变一定的条件下, 较小的比热和密度的材料可以拥有较大的绝热温变。一般来说, 铁电材料在相变温度处的热释电系数最大, 电场或应力可以移动相变温度。这为电卡制冷器件的设计提供了更多的选择。

值得注意的是, 式(7)和(8)只适用于连续相变的情形, 对于一级相变和驰豫型铁电体并不适用。对于驰豫型铁电体, 在某些温度区域存在非遍历性(non-ergodicity)问题, 即所谓的驰豫型铁电体的 “记忆效应”。在此温区, 式(7)和(8)不能使用。对于一级相变铁电体, 必须考虑相变潜热, 亦即极化强度Δ P或电位移强度Δ D的跃变。根据Clausius- Clapeyron方程, 式(7)可以写为:

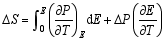(9)

由于第二项的符号与第一项的一致, 所以一级相变对电卡效应有正面的影响。

1.2 唯像理论

唯像理论被广泛地用于解释铁性材料中相变温度附近的宏观物理现象。类似于Devonshire在BaTiO3晶体里的工作, 不考虑应力与极化强度的相互作用, 弹性Gibbs自由能可以写为[ 1]:

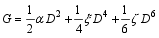(10)

这里 α= β( T- T0), β、及 ξ是与温度无关的常数。 根据式(3), Δ S=- (d G/d T) X, E, 可以得到:

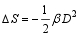(11)

于是绝热温变可以写为:

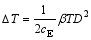(12)

根据式(11)和(12), 当材料从非极性态变到极性态时, 结构发生从无序到有序的转变, 熵要减小, 所以熵变为负值。若在绝热条件下, 电卡材料有多余的熵, 它会使材料的温度升高。即绝热温变为正。另外, 电卡效应仅与唯像系数 β和电位移强度 D(或极化强度 P)有关。这两个参数在筛选材料时需要重点考虑。

1.3 一级相变铁电体的电卡效应

一般地, 对于极性材料, 系统的熵由三部分组成, 即电子熵 Se、晶格熵 Sl和电偶极子熵 Sdi。可以认为电子熵是与电场无关的, 而其它两项是与电场相关的。在绝热条件下, 系统的熵是一个常数, 即

Δ Sdi=-Δ( Sl+ Se) (13)

这里, 晶格熵 Sl可以表示为

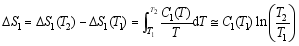(14)

假定在相变区域, 温度对比热的影响可以忽略。 另外, 假定材料的构型不变, 晶格熵和电子熵的变化必然引起材料绝热温度的变化, 即

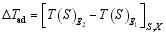(15)

现在有两种情形,

(1) 系统的熵在任何电场下都是温度的连续函数。 不考虑电子熵对系统熵的贡献, 电偶极熵可以表示成晶格比热的函数, 即[ 18]

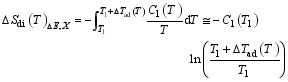(16)

上式中用到了第一中值定理。绝热温变Δ Tad可以表示为:

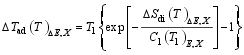(17)

如果对函数 Cl( T)/ T运用中值定理, 则有

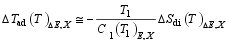(18)

可以看出, 在电偶极熵一定的条件下, 材料的绝热温变与材料的比热值成反比。

(2) 系统的熵是温度的不连续函数。此时, d P/d T不存在, Maxwell关系不能用来计算电卡效应。应该采用Clausius-Clapeyron方程, 即

(19)

式(19)左边表示电位移强度的微分是在两相平衡的情况下。将式(18)代入, 可得电卡效应的绝热温变,

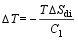(20)

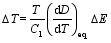(21)

假定在电场 E1和温度 TE1时, 相变的热焓为Δ EE1, 则相应的熵变为Δ SE1=Δ EE1/ TE1。同样地, 在较高的电场 E2时, 熵变为Δ SE2=Δ EE2/ TE2。

可以认为在相变区域, 比热是与温度无关的。系统的熵变可以表示为[ 18]:

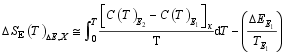(22)

通常, 在相变区域外, 电场对相变温度的影响较大, 而对比热的影响较小。因而系统的熵变可以写为:

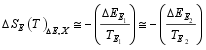(23)

式(23)表明, 系统的熵变主要来自于相变的熵。相变的热焓具有关键的作用。

系统的绝热温度要分成两部分来表示。 先定义一个特别温度 Tm, 其意义是在此温度时电场为 E1的系统熵等于电场为 E2时一级相变开始的熵。对于 TE1< T< Tm, Δ Tad( T)Δ E, X可以表示为:

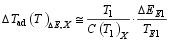(24)

对于 Tm< T< TE2, Δ Tad( T)Δ E, X可以近似表示为:

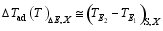(25)

进一步看到相变热焓和相变温度对一级相变铁电体的电卡效应的贡献。

1.4 铁电材料电卡效应的估计

基于式(11)和(12)和文献中 β和 D值, 可以对各种铁电材料的电卡效应进行估算。比如, 对于BaTiO3, β=6.7×105J•m/(C2•K), D=0.26 C/m2[ 2], 则Δ S=3 J/(kg•K)。考虑到比热 CE=4.07×102 J/(kg•K), Tc=107 ℃[ 2], 因而Δ T=2.8 ℃。同样地, 对于Pb(Zr xTi1- x) O3 (0< x≤0.6), β=1.88×105J•m/(C2•K), D= 0.39 C/m2[ 19, 20], 则Δ S=1.8 J/(kg•K)。考虑到比热 CE= 3.5×102 J/(kg•K)[ 20], Tc=250 ℃, 因而Δ T=2.7 ℃。

对于铁电聚合物P(VDF-TrFE), 唯像理论预示有较大的电卡效应。例如, 对P(VDF-TrFE)65/35mol%共聚物, β=3.5×107J•m/(C2•K), D=0.08 C/m2[ 21], 则Δ S=62 J/(kg•K)。考虑到比热 CE=1.4×103 J/(kg•K)[ 22], Tc=102 ℃[ 21], 因而Δ T=16.6 ℃。此外, 根据铁电到顺电的相变热( Q= TΔ S)也可以估计电卡效应。对于TGS陶瓷, 有序-无序相变热为2.0×103 J/kg, 熵变Δ S=6.1 J/(kg•K)。而对于BaTiO3, 铁电-顺电相变热为9.3×102 J/kg, 熵变Δ S=2.3 J/(kg•K)[ 2]。与此同时, 对于铁电聚合物P(VDF-TrFE)68/32mol%共聚物, 铁电-顺电相变热为2.1×104 J/kg, 熵变Δ S= 56.0 J/ (kg•K)[ 23]。

综上所述, 与铁电陶瓷相比, 铁电聚合物具有产生较大的电卡效应的潜力。

2 铁电材料中电卡效应的研究
2.1 铁电陶瓷和单晶的电卡效应

早期在铁电单晶和陶瓷的电卡效应方面的研究包括Rochelle盐、KH2PO4、SrTiO3、 Pb(Sc0.5Ta0.5)O3和Pb0.98Nb0.02(Zr0.75Sn0.20Ti0.05)0.98O3。有趣的是, 以往所有单晶和陶瓷的绝热温变都小于1.5 ℃。直到1981年, Tuttle和Payne在Pb0.98Nb0.02(Zr0.75Sn0.20Ti0.05)0.98O3陶瓷中161 ℃得到2.5 ℃的绝热温变, 所加电场为3 MV/m。然而熵变只有2.88 J/(kg•K)[ 24]。他们同样采用Maxwell关系来计算电卡效应。最近Moya等报道了BaTiO3单晶的电卡效应。他们发现, 尽管BaTiO3单晶的绝对温变小于1 ℃(130 ℃, E=1.2 MV/m), 但是其单位电场的绝热温变(Δ T/ Δ E)和潜热(|Δ Q/Δ E|)却分别达到2.2 Km/MV和2087.5 Jm/(kg•MV)[ 25], 远大于其它铁电材料。对于一级相变材料来说, 由于相变潜热的存在, 这样的结果是可以理解的。

2.2 铁电薄膜的电卡效应

实际上影响铁电单晶和铁电陶瓷的电卡效应的关键因素在于它们的击穿电场强度较低。体材料中的缺陷是导致击穿电场低的主要原因。击穿电场与材料厚度的关系可以表示为[ 26]:

(kV/cm) (26)

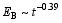
所以人们把目光转向铁电薄膜。2006年, Mischenko等[ 27]报道了溶胶-凝胶法制备的Pb (Zr0.95Ti0.05)O3反铁电薄膜中的电卡效应。薄膜的厚度为350 nm, 测试电场为48 MV/m, 温度为226 ℃(铁电-顺电相变温度为222 ℃)。采用Maxwell关系式计算电卡效应, 得到绝热温变为12 ℃。进一步可以得到其熵变为8 J/(kg•K)。此工作的缺点是工作温度偏高, 熵变值偏小。

为了降低工作温度, Correia等用Pb(Zr0.8Ti0.2)O3种籽层在Pt/Ti/TiO2/SiO2/Si基片上生长了Pb (Mg1/3Nb2/3) O3- PbTiO3(PMN-PT)薄膜。在25 ℃时得到绝热温变为9 ℃, 等温熵变为9.7 J/(kg•K)[ 28]。有意思的是测试温度不在相变点以上, 而是接近于去极化温度(18 ℃)。 并且大的电卡效应只是出现在加电场放热的时候。Correia等[ 28]认为电卡效应来自于从稳态和亚稳态的极性纳米区域到非极性纳米区域的转变。在PMN-PT和(PbLa)(ZrTi)O3(PLZT)驰豫型铁电体单晶和陶瓷中已经观察到场诱相变。由于非遍历性的影响, 热历史对驰豫型铁电体的场诱相变具有很重要的影响。场诱相变能产生较大的感应极化, 从而产生较大的热释电系数(d P/d T)及较大的电卡效应Δ S和Δ T。此外, 驰豫型铁电体的平均相变温度在室温附近, 应用起来非常方便。

对于铁电薄膜, 衬底的影响必须考虑, 因为衬底和薄膜之间由于晶格失配会产生应力或应变, 从而改变薄膜的边界条件。考虑衬底因素后的弹性Gibbs自由能可以表示为[ 29]：

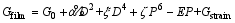(27)

其中,

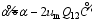(28)

及

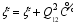(29)

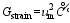
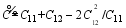
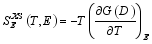是修饰后的唯像系数。 是没有极化时的应变能。 , Cij是在一定极化强度时的弹性常数, Qij是立方相的电致伸缩系数, um是平面内的应变失配度。 在式(28)中, 相变温度随应变失配度线性变化。式(29)表示二维夹持对唯像系数的影响。由于基片影响产生的过量的熵和比热可以表示为:

(30)

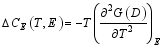(31)

式(31)表明, 对于BaTiO3薄膜, 良好的横向夹持会使BTO的相变从不连续变为连续。相应地极化强度和比热在相变区域也会减小。从式(28)和(29)可知, 改变应变失配度, 可以改变电卡效应的性质。

本课题组在掺镧的锆钛酸铅(PLZT-(Pb1- xLa x)(Zr1- yTi y)O3) (8/65/35)薄膜中观察到了绝热温变达40 ℃, 等温熵变达50 J/(kg•K)[ 30]。对铁电薄膜来说, 存在的问题是薄膜只能生长在Pt/Ti/SiO2/Si等衬底上, 这给电卡制冷器件的设计带来非常大的麻烦。此外, 薄膜材料在强场下通常会产生较大的漏电流, 因此焦耳热也会较大。

2.3 铁电聚合物的电卡效应

2.3.1 直接法测量电卡效应

到目前为止, 大部分报道的电卡效应都是用Maxwell关系式计算出来的, 称之为间接法。直接法就是直接测量电卡材料产生的等温熵变或绝热温变。直接法又可分为绝对直接法和相对直接法。前者是 直接测量电卡效应的等温熵变或绝热温变, 后者是 通过一个参比电阻来得到电卡材料的电卡效应值。

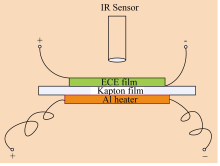
在磁卡效应的研究中, 报道了几种直接测量的方法, 例如热电偶法[ 31]、热温度计[ 32]及量热仪[ 33]。本课题组采用一种高精度的量热仪来测量电卡效 应[ 34]。样品的温度信号由一个小的热敏电阻来测量。方形脉冲信号由函数发生器产生, 并施加在电卡材料上。脉冲宽度或频率的选择基于样品与周围环境的热平衡时间。由于电卡效应是一种快响应过程(在几十毫秒或更小的量级, 取决于施加的电场强度), 可以采用一个简单的描述热过程的零维模型来计算相关参数。在热驰豫过程中, 样品系统的温度 T( t)可以表示为:

(32)

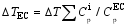
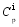
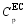
这里 Tbath为样品的初始温度, Δ T为施加电场后样品温度的变化。测量的整个样品系统的温度变化 。这里 为每个子系统的比热, 为电卡材料及电极的比热。对于一级相变材料, Δ T由式(24)或(25)确定。

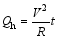
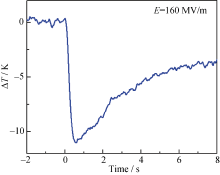
本课题组还设计了新的测量电卡效应的装置[ 30]。利用此装置, 电卡材料产生的热量与参考电阻产生的热量进行比较, 进而得到电卡材料产生的熵变。当一个脉冲信号 V加在一电阻 R上 t时间, 电阻产生的焦耳热为 。该热量将在电卡材料表面产生温度变化为Δ Theater。它可以通过红外温度探测器进行非接触测量(见图1)。如果电卡材料在电场作用下产生温度变化为Δ TECE, 其对应的热量 QECE与电阻产生的焦耳 Qh热成比例。即, Qh/( TΔ SECE)= Δ Theater/Δ TECE=1/ η( T), 且Δ SECE=( Qh/ T)• η( T), 因此Δ TECE= [ Qh/( CE ρU)]• η( T)。这里 CE、 ρ和 U分别为电卡材料的比热、密度和有效体积。 η( T)由Δ Theater和Δ TECE的峰值之比确定, 两者的峰分布可以在不同的时间由示波器记录下来。

图1 电卡效应测试装置[ 30]Fig. 1 Electrocaloric effect measurement setup[ 30]

图2是直接法测试得到的曲线。 电卡材料为高能电子辐照过的聚(偏氟乙烯-三氟乙烯)68/32mol%共聚物。测试温度为36 ℃。施加电场( E=160 MV/m)时, 材料温度升高; 撤除电场时, 材料温度下降。经过一段时间后, 材料回复到环境温度。

图2 采用直接法得到的电卡效应温度变化与时间的关系电卡材料为高能电子辐照过的聚(偏氟乙烯-三氟乙烯) 68/32mol%共聚物Fig. 2 ECE temperature change as a function of time using the direct measurement method. ECE material is high-energy electron irradiatiated P(VDF-TrFE)68/32mol% copolymer

2.3.2 铁电聚合物厚膜的电卡效应

采用高精度的量热仪测量了P(VDF-TrFE) 55/45mol%共聚物厚膜(4~7 μm)。共聚物采用溶液-浇铸法制备, 并在135~140 ℃进行热处理。电卡效应测量的结果如图3所示。采用Maxwell关系式计算的结果也有两个点(空心点)画在图3上[ 35]。可以

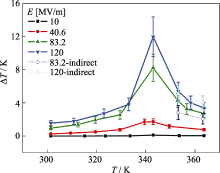图3 P(VDF-TrFE)55/45mol%共聚物的电卡效应[ 30]Fig. 3 Electrocaloric effect of P(VDF-TrFE)55/45mol% copolymers[ 30]

看出, 间接法得到的结果与直接法得到的结果一致。它们在相变温度以上可以比较, 随温度变化的趋势也一致。在相变温度处的电卡效应值最大。这些结果与唯像理论的结果也是一致的。

本课题组运用自己制造的电卡分析仪测量了高能电子辐照的P(VDF-TrFE)68/32mol%共聚物。 经高能电子辐照后, 共聚物变成了弛豫型铁电体。在36 ℃和160 MV/m电场作用下, 该共聚物表现出绝热温变为20 ℃, 熵变为95 J/(kg•K)的电卡效应[ 30]。与此同时, 电卡效应随温度变化的弱关系也基本得到了。

本课题组对一级相变铁电聚合物的电卡效应也进行了测试。通过不同程度的辐照, P(VDF-TrFE) 65/35 mol%共聚物能从驰豫型铁电体向一级相变正常铁电体变化。在50 ℃和180 MV/m电场作用下, 该共聚物表现出本征绝热温变为35 ℃, 本征熵变为160 J/(kg•K)的电卡效应[ 36]。

2.4 铁电多层陶瓷电容器的电卡效应

铁电多层陶瓷更适合应用于电卡器件。一方面, 电卡材料在制成器件时需要具有一定的功率。另一方面, 材料要有较高的击穿电场强度。此外, 电卡材料不能像薄膜材料那样带有基片, 因而多层结构将是器件应用的方向。

随着电子信息技术的快速发展, 陶瓷电容器的片式化已经占有电容器市场的绝大部分。 经过几十年的发展历程, 到目前为止, 多层片式陶瓷电容器的制备工艺已经非常成熟。 片式电容器的外形尺寸已从0805(2 mm×1.3 mm)到更小的0603、0504、0402、0201 及01005(0.4 mm×0.2 mm)。电极层和介电层的厚度已小于1 μm[ 37]。

最近关于以BaTiO3为基的多层陶瓷电容器的电卡效应的报道越来越多。Kar-Narayan等报道BaTiO3多层陶瓷电容器(Y5V)的直接测量绝热温度为~0.5 ℃(340 K, 电场30 MV/m)[ 38]。白洋等[ 39]也报道了BaTiO3多层陶瓷电容器的ECE测量结果, 他们得到的结果为Δ T=7.1 ℃, Δ S=10.1 J/(kg•K)(在80 ℃ 温度及80 MV/m电场下)。他们发现电卡效应依赖于电场在上升或下降时的变化率。即调节电场上升和下降的速度, 可以得到静负热流, 从而实现制冷。Kar-Narayan等[ 38]认为BaTiO3多层陶瓷电容器的电卡效应小的原因在于: 1)BaTiO3材料本身的电卡效应(如我们上面的唯像理论预测)就小; 2)电场不能加到100~ 200 MV/m; 3)电容器的改性有利于电容性能, 不利于电卡效应; 4)电卡活性区域由非活性的材料包围, 进一步压抑了相变, 也减小了电卡效应。最近, Defay等[ 40]观察到边沿的夹持作用对ECE有明显的影响。

3 电卡效应研究的应用前景

对电卡效应重新燃起的热潮源于发表在Science杂志的关于PZT和P(VDF-TrFE)薄膜的两项工作[ 23, 27]。目前研究工作已经涵盖了无机铁电反铁电单晶、陶瓷、薄膜、厚膜、有机铁电薄膜、厚膜以及铁电液晶等, 数种材料表现出了诱人的应用前景。铁电聚合物的绝热温变和等温熵变仍然高于其它材料; 驰豫型铁电体中具有纳米无序态及室温平均相变温度。铁电多层陶瓷也表现出较高的电卡效应的累积效应。一级相变单晶BaTiO3具有非常高的电卡效率(Δ Q/Δ E, Δ T/Δ E)。关于铁电制冷器件方面, 早期Sinyavsky[ 41]等用铁电陶瓷进行了电卡制冷器件的尝试, 得到了约4 ℃的冷热端温差。最近Gu等采用辐照后的P(VDF-TrFE)多层膜以及一种往复运动蓄热的方式, 得到了约6 ℃的冷热端温差[ 42], 表现出诱人的应用前景。随着众多在多层结构设计、热流开关、新制冷材料的不断开拓, 制备可实用化的制冷器件指日可待。

4 结束语

本文介绍了电卡效应的概念、研究历史、 热力学唯像理论和一级相变的电卡效应理论。 驰豫型铁电体聚合物和一级相变聚合物材料具有较大的电卡效应。BaTiO3单晶具有非常高的电卡效率(Δ Q/Δ E, Δ T/Δ E)。 多层陶瓷电容器在工艺上提供了向实用器件迈进的可行性。最近在电卡器件研究的报道进一步提高了向实用化器件转化的可能性。

The authors have declared that no competing interests exist.

参考文献
1 Lines M, Glass A. Principles and Applications of Ferroelectrics and Related Materials. Oxford: clarendon Press, 1977. [本文引用:3]
2 Fatuzzo E, Merz W J. Ferroelectricity. Amsterdam: North-Holland , 1967. [本文引用:4]
3 Mitsui T, Tatsuzaki I, Nakamura E. Introduction to the Physics of Ferroelectricity. London: Gordon and Breaeh, 1976. [本文引用:1]
4 Kobeko P, Kurtschatov J. Dielectric properties of Rochelle salt crystal. Z. Physik, 1930, 66: 192-205. [本文引用:1] [JCR: 1.212]
5 Wiseman G G, Huebler D A. Electrocaloric effect in ferroelectric rochelle salt. Phys. Rev. , 1963, 131(5): 2023-2027. [本文引用:1] [JCR: 7.37]
6 Benepe J W, Reese W. Electronic studies of KH2PO4. Phys. Rev. B, 1971, 3(9): 3032-3039. [本文引用:1]
7 Lawless W N. Specific heat and electrocaloric properties of KTaO3 at low temperatures. Phys. Rev. B, 1977, 16(1): 433-439. [本文引用:1]
8 Hegenbarth E. Studies of the electrocaloric effect of ferroelectric ceramics at low temperatures. Cryogenics, 1961, 1(4): 242-250. [本文引用:1] [JCR: 0.669]
9 Lawless W N. Recent topics in ferroelectric properties at low temperatures. Ferroelectrics, 1980, 24(1): 327-335. [本文引用:1] [JCR: 0.391]
10 Strukov B A. Electrocaloric effect in single-crystal triglycine sulfate. Sov. Phys. Crystallogr. , 1967, 11: 757. [本文引用:1] [JCR: 0.469]
11 Pecharsky V K, Gschneidner Jr KA. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. , 1997, 78(23): 4494-4497. [本文引用:1] [JCR: 7.37]
12 Morellon L, Magen C, Algarabel P A, et al. Magnetocaloric effect in Tb5(SixGe1-x)4. Appl. Phys. Lett. , 2001, 79(9): 1318-1320. [本文引用:1] [JCR: 3.844]
13 Wada H, Tanabe Y. Giant magnetocaloric effect of MnAs1-xSbx. Appl. Phys. Lett. , 2001, 79(20): 3302-3304. [本文引用:1] [JCR: 3.844]
14 Hu F X, Shen B G, Sun J R, et al. Influence of negative lattice expansion on magnetic entropy change in the compounds LaFe11. 4Si1. 6. Appl. Phys. Lett. , 2001, 78(23): 3675-3677. [本文引用:1] [JCR: 3.844]
15 Fujita A, Fujieda S, Hasegawa Y, et al. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(FexSi1-x)13 compounds and their hydrides. Phys. Rev. B, 2003, 67(10): 104416-1-12. [本文引用:1]
16 Tegus O, Brück E, Buschow K H J, et al. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature, 2002, 415(6868): 150-152. [本文引用:1] [JCR: 36.28]
17 Albertini F, Canepa F, Cirafici S, et al. Composition dependence of magnetic and magnetothermal properties of Ni-Mn-Ga shape memory alloys. J. Magn. Magn. Mater. , 2004, 272-276: 2111-2112. [本文引用:1] [JCR: 1.78]
18 Pecharsky V K, Gschneidner Jr K A, Pecharsky A O, et al. Thermodynamics of the magnetocaloric effect. Phys. Rev. B, 2001, 64(14): 144406-1-10. [本文引用:2]
19 Amin A, Cross L E, Newnham R E. Calorimetric and phenomenological studies of the PbZrO3-PbTiO3 system. Ferroelectrics, 1981, 37(1-4): 647-650. [本文引用:1] [JCR: 0.391]
20 Amin A, Newnham R E, Cross L E. Phenomenological and structural study of a low-temperature phase-transition in the PbZrO3- PbTiO3 system. J. Solid State Chem. , 1981, 37(2): 248-255. [本文引用:2] [JCR: 2.159]
21 Furukawa T. Phenomenological aspect of a ferroelectric vinylidene fluoride / trifluoroethylene copolymer. Ferroelectrics, 1984, 57(1-4): 63-72. [本文引用:2] [JCR: 0.391]
22 Furukawa T, Nakajima T, Takahashi Y. Factors governing ferroelectric switching characteristics of thin VDF/TrFE copolymer films. IEEE Trans. Diel. Ele. Ins. , 2006, 13(5): 1120-1131. [本文引用:1]
23 Neese B, Chu B J, Lu S G, et al. Large electrocaloric effect in ferroelectric polymers near room temperature. Science, 2008, 321(5890): 821-823. [本文引用:2]
24 Tuttle B A, Payne D A. The effect of microstructure on the electrocaloric properties of Pb(Zr, Sn, Ti)O3 ceramics. Ferroelectrics, 1981, 37(1-4): 603-606. [本文引用:1] [JCR: 0.391]
25 Moya X, Stern-Taulats E, Crossley S, et al. Giant electrocaloric strength in single-crystal BaTiO3. Adv. Mater. 2013, 25(9): 1360-1365. [本文引用:1] [JCR: 13.877]
26 Gerson R, Marshall T C. Dielectric breakdown of porous ceramics. J. Appl. Phys. , 1959, 30(11): 1650-1653. [本文引用:1] [JCR: 0.771]
27 Mischenko A S, Zhang Q, Scott J F, et al. Giant electrocaloric effect in thin-film PbZr0. 95Ti0. 05O3. Science, 2006, 311(5765): 1270-1271. [本文引用:2]
28 Correia T M, Young J S, Whatmore R W, et al. Investigation of the electrocaloric effect in a PbMg1/3Nb2/3O3-PbTiO3 relaxor thin film. .Appl. Phys. Lett, 2009, 95(18): 182904-1-3. [本文引用:2] [JCR: 3.844]
29 Akcay G, Alpay S P, Mantese J V, et al. Magnitude of the intrinsic electrocaloric effect in ferroelectric perovskite thin films at high electric fields. Appl. Phys. Lett. , 2007, 90(25): 252909-1-3. [本文引用:1] [JCR: 3.844]
30 Lu S G, Rožič B, Zhang Q M, et al. Organic and inorganic relaxor ferroelectrics with giant electrocaloric effect. Appl. Phys. Lett. , 2010, 97(16): 162904-1-3. [本文引用:3] [JCR: 3.844]
31 Dinesen A R, Linderoth S, Mørop S. Direct and indirect measurement of the magnetocaloric effect in a La0. 6Ca0. 4MnO3 ceramic perovskite. J. Magn. Magn. Mater. , 2002, 253(1/2): 28-34. [本文引用:1] [JCR: 1.78]
32 Gopal B R, Chahine R, Bose T K. A sample translatory type insert for automated magnetocaloric effect measurements. Rev. Sci. Instrum. , 1997, 68(4): 1818-1822. [本文引用:1] [JCR: 1.367]
33 Tocado L, Palacios E, Burriel R. Direct measurement of the magnetocaloric effect in Tb5Si2Ge2. J. Magn. Magn. Mater. , 2005, 290-291(Part 1): 719-722. [本文引用:1]
34 Yao H, Ema K, Garland C W. Nonadiabatic scanning calorimeter. Rev. Sci. Instrum. , 1998, 69(1): 172-178. [本文引用:1] [JCR: 1.367]
35 Lu S G, Rožič B, Zhang Q M, et al. Enhanced electrocaloric effect in ferroelectric poly (vinylidene-fluoride/trifluoroethylene) 55/45 mol% copolymer at ferroelectric-paraelectric transition. Appl. Phys. Lett. , 2011, 98(12): 122906-1-3. [本文引用:1] [JCR: 3.844]
36 Li X Y, Qian X S, Gu H M, et al. Giant electrocaloric effect in ferroelectric poly(vinylidene fluoride-trifluoroethylene) copolymers near a first-order ferroelectric transition. Appl. Phys. Lett. , 2012, 101(13): 132903-1-3. [本文引用:1] [JCR: 3.844]
37 干福熹主编. 信息材料二十一世纪新材料丛书. 天津: 天津大学出版社, 2000. [本文引用:1]
38 Karayan S, Mathur N D. Direct and indirect electrocaloric measurements using multilayer capacitors. J. Phys. , D: Appl. Phys. , 2010, 43(3): 032002-1-5. [本文引用:2] [JCR: 2.544]
39 Bai Y, Zheng G P, Ding K, et al. The giant electrocaloric effect and high effective cooling power near room temperature for BaTiO3 thick film. J. Appl. Phys. , 2011, 110(9): 094103-1-3. [本文引用:1] [JCR: 0.771]
40 Defay E, Crossley S, Kar-Narayan S, et al. The electrocaloric efficiency of ceramic and polymer films. Adv. Mater. 2013, 25(24): 3337-3342. [本文引用:1] [JCR: 13.877]
41 Sinyavsky Y V, Brodyansky V. Experimental testing of electrocaloric cooling with transparent ferroelectric ceramic as a working body. Ferroelectrics, 1992, 131(1-4): 321-325. [本文引用:1] [JCR: 0.391]
42 Gu H M, Qian X S, Li X Y, et al. A chip scale electrocaloric effect based cooling device. Appl. Phys. Lett. , 2013, 102(12): 122904-1-4. [本文引用:1] [JCR: 3.844]