利用第一性原理热力学方法, 能够评估相对复杂系统的热力学稳定性。一般来说, 其要点是确定总体的Gibbs能量与其组成原子化学势的关系。基于准二元固溶方法, 可以将铋层状化合物当作最低层稳定相和钙钛矿这两个单元的固溶体来处理。根据化学势平衡, 两个单元的化学势等于其组成原子的化学势之和, 例如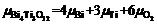,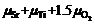。复杂体系总体的Gibbs能量本该严格地等于单质元素化学势之和, 此时可约化为两个参考单元的化学势之和。这种推导是基于特殊的层状堆叠特性, 它只改变体系的参考能量。

本工作只研究三个典型的A位无序的铋层状系列: CaBi₂Nb₂O₉- nNaNbO₃ (CBN- nNN)、Bi₄Ti₃O₁₂- nSrTiO₃ (BiT- nST)和Bi₄Ti₃O₁₂- nCaTiO₃ (BiT- nCT), n代表插入最低层相中的钙钛矿层数, m-n即是最低层相的层数。对于BiT- nMT系列, 其组成单元是3层相BiT和钙钛矿单元MT, 化学反应式可写作

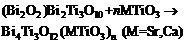(1)

因此, 总体的Gibbs能量可表示为

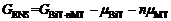(2)

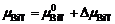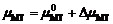G_{BiT- nMT}是终态的Gibbs能量, 包含直接由第一性原理计算得到的内能 E_{BiT- nMT}和熵的贡献。本工作中熵包含两部分: 构型熵和振动熵, 前者与A位无序导致的不同构型数目可用Boltzmann方程- TΔ S= k_B Tln Ω相联系, 其中 Ω是构型数, 温度固定在 T=1273 K; 后者可根据软模理论粗略估算。 μ_BiT和 μ_MT分别是BiT和MT的化学势,和。通常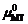是0 K下钙钛矿相的第一性原理总能。本工作是为了阐明Gibbs能量与 μ_MT的依赖关系, 由此判定不同相的相对稳定性。

本工作选择最低层相作为参考态, 其总体Gibbs能量为, 其中,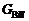与0 K下的化学势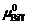相等。将化学势的定义式代入公式(2), 可得到相对Gibbs能量

. (3)

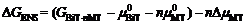
右边第一项可写作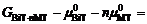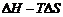, H即为体系的形成焓。因此, 通过评估不同结构的相对Gibbs能量及其对钙钛矿单元化学势的依赖关系, 可以判定不同相之间的竞争关系。物理上, 存在一个化学势 μ_MT的有效范围, 使得它低于其对应纯相的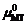, 否则整个体系在热力学上是不稳定的, 因而可以通过此差值相对大小来描述实验上各相的相对稳定性, 总的稳定范围约在-0.3~0 eV之间, 这是由相对Gibbs能量的范围所决定的。

以上方法同样可以应用于另一个系列CaBi₂Nb₂O₉- nNaNbO₃, 其化学反应式和相对Gibbs能量分别为

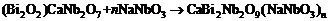(4)

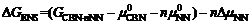(5)

唯一不同的是终态构型个数, 这将导致这两种系列具有不同的构型熵。

在第一性原理密度泛函理论计算中, 交换关联效应采用PBE广义梯度近似(GGA)处理^{[ 14]}, 所有电子结构和总能计算都是基于投影缀加波(PAW)方法。平面波截断能设置为450 eV, 而电子结构自洽的能量收敛判据设为1×10^-4eV。所有计算都采用3×3×6的Monkhors-Pack K点网络^{[ 15]}; 所有原子弛豫到能量平衡位置直到作用在它们上的Hellmann-Feynman力小于0.2 eV/nm; 所有化合物的晶胞形状、体积和原子内坐标都弛豫至最稳定状态。

为阐明铋层状结构中不同相的竞争关系, 本工作建立了不同相的相对Gibbs能量与钙钛矿化学势的函数关系, 如图1。

本工作中化学势被当作描述体系对环境依赖的一个有效参数。当化学势足够低时, 所有相中, 参考相(图1中黑色实线标记)是热力学最稳定的。随着化学势增加, 出现相竞争。研究结果表明, 当化学势升高至相对高的值时, 大约为-0.1 eV, 三个系列中的所有相都比参考相更加稳定。

对于CBN- nNN系列, 当 μ_NN升至大约-0.15 eV时, 3层相具有最低相对Gibbs能量, 紧接着4层相和6层相依次变成最稳定, 直到 μ_NN接近零, 7层相才达到最稳定。在整个过程中, 5层相始终相对不稳定。BiT- nCT系列的情况也类似, μ_CT达到-0.2 eV时, 4层相最稳定, 5层相在极窄的范围内稳定后就被6层相取代, 最终也是7层相成为最稳定相。BiT- nST系列中, 4层、5层和7层相依次成为最稳定, 6层相由于具有较高的相对Gibbs能量, 无法与其他相竞争。

另外, 研究结果还能给出最稳定相存在的范围,有些相在相对较大的化学势范围内最稳定, 而有些相的稳定范围则相对较窄。当化合物的层数增加时, 这些相在较高的化学势下稳定, 其范围也很窄, 这与通常认为的高层相倾向于不稳定的观点是一致的。

在实验合成陶瓷样品过程中, 某些样品很难得到纯相。CBN- nNN系列的XRD结果表明, 3层相样品中包含4层相, 而5层相样品中有等量的5层、6层和7层相^{[ 7]}。本研究结果可以给出相应的解释: 由图1(a), 3层相在一个相对较小的范围内最稳定, 实验条件稍微改变, 就可能达到4层相最稳区域。5层相被证明是相对不稳定的, 而6层相和7层相在化学势较高的区域相对稳定, 样品中混入6层和7层相时, 这种无序的共生结构具有比5层相更低的相对Gibbs能量, 因此5层相样品更倾向于以这种混合相的形式存在。本计算结果表明(见图1(b)), BiT- nCT系列7层以下的相在某特定条件下都能达到最稳定, 实验上能够合成到6层相^{[ 16]}, 而7层相还有待合成。从BiT- nST的HRTEM图像可知^{[ 8]}, 6层相比其他相存在更多的无序区域。由图1(c)可知, 6层相相对于其它相总是不稳定的, 而样品中的无序结构将增大熵的贡献, 从而使得相对Gibbs能量降低。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 不同相的相对Gibbs能量与钙钛矿化学势的函数关系Fig. 1 Gibbs energy of different phases relative to the elemental phase as a function of chemical potential of Perovskite unitsThose different phases are indicated by different colors and different types of line

相对Gibbs能量中温度依赖的部分主要来自于熵的贡献。前面提到, 熵可以分为: 构型熵和振动熵。构型熵是由于原子可以从一个晶格移动到另一个, 而振动熵来自于每个原子在其平衡位置的振动。在铋层状这种特殊结构中, 前者是钙钛矿A位的原子占位无序导致的, 而后者主要来自于B位离子的振动。

2.2.1 构型熵

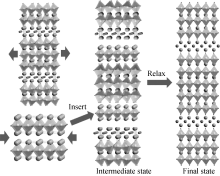
本工作提出了一种堆叠模型来描述铋层状材料的理想生长过程(见图2)。将最低层相拉伸, 同时压缩钙钛矿至相同的晶格常数, 然后将钙钛矿插入到最低层相中形成中间相, 最后通过优化原子位置与化学成键, 将中间相弛豫至终态。值得注意的是, 有两种不同的原子占据着A位格点, 所有这些原子占据的几率是相同的, 由此, 这样的A位无序提供了相对Gibbs能量中构型熵的贡献。探索随温度变化的相竞争演化具有重要意义。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 铋层状材料生长的理想堆叠模型Fig. 2 Stacking model of growth of bismuth layered structure

图3(a)给出了CBN- nNN系列随温度变化的相竞争演化, 当温度等于0 K时, 没有熵的效应, 几乎不存在相竞争现象, 参考相是最稳定相, 占据-0.3~ 0 eV的绝大部分区域。其他相被局限在很窄的范围内, 且只有6层相是最稳定的。当温度升高时, 其他相变成最稳定的机会增加, 相竞争更加激烈, 当温度达到1273 K时, 3层相、4层相和7层相也在特定范围内成为最稳定相。如前所述, 5层相始终处于相对不稳定状态。其他两个系列也表现出相似的相竞争演化趋势, 见图3(b)和3(c), 随着温度升高, 参与竞争的相也增加, 高层相的稳定范围也扩大, 这也证明了相竞争现象是由熵驱动的。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 三个系列随温度升高(从0增加至1273 K)的相竞争演化Fig. 3 Phase competition evolution of the above three series as temperature increases from 0 K to 1273 KPhases with different number of layers are indicated by different colors, and phases at different temperature are indicated by different types of line, dash line for those at 0 K and solid line for those at 1273 K

2.2.2 振动熵

上述讨论只包含了原子的取代交换, 而未涉及原子振动带来的振动熵贡献。有报道指出, 在二元合金中两个相的振动熵之差的数量级约为0.1到0.2 k_B/原子, 与构型熵的典型值(最大0.693k_B /原子)相当^{[ 17]}。而对于复杂的A位无序的铋层状氧化物, 我们还不清楚振动熵的贡献为多少以及它在多大程度上影响相竞争。

由于计算复杂铋层状系统的整个声子谱是十分困难的, 在此利用一种粗略而有效的近似来估算系统的振动熵贡献。首先定义振动熵对总体的Gibbs能量的贡献来自于堆叠模型中终态和中间态结构的熵之差。假设相应的终态和中间态的熵差由某一支导致B位原子离心位移的软模频率改变决定的, 而其他声子模保持不变。对于典型的钙钛矿体系, 变软的那支声子模频率在100~200 cm^-1之间, 在终态结构中这支模的频率会降低至20 cm^-1左右。根据两相的振动熵之差的公式,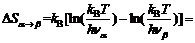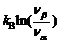, 可以估算振动熵对于总体的Gibbs能量的贡献约为0.18~0.25 eV之间, 与构型熵相当。然而, 在本工作的近似中, 假设了每个钙钛矿单元是完全相同的。随着层数增加, 虽然原胞中原子个数增加, 但其振动对熵的贡献是不变的, 就如同在原胞和由若干原胞组成的超胞中计算的声子谱对熵的贡献是相同的, 因此一个系列中每个相的振动熵的贡献都应该是相同的, 那么这个额外的贡献不会在本质上改变整个相竞争图像, 而是在构型熵的基础上增加低层相的最稳定范围。这与实验上所观察到低层相更容易制备纯相也是相符的。